Libreria 3 D

Ho portato in Livecode una libreria 3D che era scritta in Rebol.

E' stato un esercizio interessante per capire il funzionamento della grafica 3D e ho scritto i seguenti appunti per spiegare i funzionamenti base del 3D sui computer. Buona lettura.

Concetti di base

Prima di tutto un po' di semplice geometria. Ogni punto dello spazio puo' essere rappresentato da tre coordinate X, Y, Z; che in forma matriciale si scrive:

` [(X),(Y),(Z)] `

Questa e' una matrice 3x1 (tre righe ed una sola colonna). Nelle operazioni grafiche si usa quasi sempre la notazione matriciale, perche' fa capire a colpo d'occhio cosa si fa. Un'equazione fra matrici di una sola riga equivale sempre ad almeno tre lunghissime equazioni normali: una per ogni coordinata. Scrivere in forma matriciale fa risparmiare tempo e capire piu' semplicemente le operazioni che si eseguono.

Ora la questione si complica un pochino: per come sono costituite le matrici per le operazioni grafiche, cioe' di 4 righe e 4 colonne (4x4), serve che la matrice che indica le coordinate dei nostri punti sia fatta almeno di 4 righe; altrimenti non e' possibile moltiplicarle correttamente tra loro. Per questo motivo si aggiunge un 1 che e' ininfluente sulle coordinate, ma permette di compiere correttamente le operazioni fra matrici. Ecco quindi come scrivere la matrice delle coordinate di un punto in grafica 3D:

` [(X),(Y),(Z),(1)] `

Moltiplicazione tra matrici

L'uso delle matrice semplifica la scrittura delle equazioni, perche' ad esempio il seguente prodotto:

` [(a, b, c, d), (e, f, g, h), (i, l, m, n), (p, q, r, s)] . [(x), (y), (z), (1)] = [(x_2), (y_2), (z_2), (w)]`

significa fare le seguenti quattro operazioni:

` x_2 = a x + b y + c z + d`
` y_2= e x + f y + g z + h`
` z_2 = i x + l y + m z + n`
` w = p x + q y + r z + s`

Trasformazioni geometriche

Le seguenti trasformazioni servono per spostare gli oggetti e preparare la scena che volete ritrarre. Con le seguenti trasformazioni potete spostare tutti gli oggetti come piu' vi piace.

Prima di tutto vediamo la matrice identita', questa matrice moltiplicata per le coordinate dei punti, li lascia inalterati. La matrice identita' ha tutti 1 sulla diagonale principale e 0 in tutte le altre posizioni. In termini matriciali si puo' scrivere:

` [(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1) ] * [(X),(Y),(Z),(1)] = [(X),(Y),(Z),(1)] `

Ora vediamo le traslazioni. Abbiamo una traslazione quando voglio spostare un punto (P1_X,P1_Y,P1_Z) di una certa distanza che puo' essere scomposta lungo le tre direzioni (d_x,d_y,d_z) e dopo la traslazione il punto si ritrovera' in una nuova posizione (P2_X,P2_Y,P2_Z). In termini matriciali abbiamo la seguente operazione:

` [(1,0,0,d_x),(0,1,0,d_y),(0,0,1,d_z),(0,0,0,1)] * [(P1_X ),(P1_Y ),(P1_Z ), (1)] = [(P2_X) ,(P2_Y),(P2_Z),(1)] `

Per le rotazioni la questione e' piu' spinosa, qualunque rotazione, per quanto complessa, puo' essere scomposta come una somma di rotazioni attorno ai tre assi principali (x,y,z), quindi c'e' una matrice da applicare per la rotazione su ogni asse.

La matrice per la rotazione intorno all'asse X di un angolo ` alpha ` e' la seguente:

` [(1,0,0,0),(0,cos(alpha),-sin(alpha),0),(0,sin(alpha),cos(alpha),0),(0,0,0,1)] * [(P1_X ),(P1_Y ),(P1_Z ), (1)] = [(P2_X) ,(P2_Y),(P2_Z),(1)] `

La matrice per la rotazione intorno all'asse Y di un angolo ` beta ` e' la seguente:

` [(cos(beta),0,sin(beta),0),(0,1,0,0),(-sin(beta),0,cos(beta),0),(0,0,0,1)] * [(P1_X ),(P1_Y ),(P1_Z ), (1)] = [(P2_X) ,(P2_Y),(P2_Z),(1)] `

La matrice per la rotazione intorno all'asse Z di un angolo ` gamma ` e' la seguente:

` [(cos(gamma),-sin(gamma),0,0),(sin(gamma),cos(gamma),0,0),(0,0,1,0),(0,0,0,1)] * [(P1_X ),(P1_Y ),(P1_Z ), (1)] = [(P2_X) ,(P2_Y),(P2_Z),(1)] `

Per scalare i punti, cioe' avvicinarli o allontanarli dall'origine, questa e' la matrice:

` [(a,0,0,0),(0,b,0,0),(0,0,c,0),(0,0,0,1)] * [(P1_X ),(P1_Y ),(P1_Z ), (1)] = [(P2_X) ,(P2_Y),(P2_Z),(1)] `

Ora vediamo come è semplice combinare tutte le operazioni insieme, vedete come l'espressione con la notazione matriciale risulti molto compatta:

` [(1,0,0,d_x),(0,1,0,d_y),(0,0,1,d_z),(0,0,0,1)] * [(1,0,0,0),(0,cos(alpha),-sin(alpha),0),(0,sin(alpha),cos(alpha),0),(0,0,0,1)] * [(cos(beta),0,sin(beta),0),(0,1,0,0),(-sin(beta),0,cos(beta),0),(0,0,0,1)] * [(cos(gamma),-sin(gamma),0,0),(sin(gamma),cos(gamma),0,0),(0,0,1,0),(0,0,0,1)] * [(a,0,0,0),(0,b,0,0),(0,0,c,0),(0,0,0,1)] * [(P1_X ),(P1_Y ),(P1_Z ), (1)] = [(P2_X) ,(P2_Y),(P2_Z),(1)] `

Se avessimo scritto le equazioni in forma normale per ogni coordinata, non sarebbe bastata una pagina intera formato A4.

Come passare dal 3D al 2D

Lo schermo del PC e' una superficie piana a due dimensioni, mentre uno spazio tridimensionale ne ha tre: come facciamo a perdere una dimensione senza fare un pasticcio? Bisogna andare per gradi per capire il procedimento. Prima di continuare con le formule, vediamo gli aspetti concettuali.

Iniziamo con l'immaginare una scena con un oggetto da rappresentare sullo schermo, ad esempio un cubo rosso e una sfera blu (tutte le immagini seguenti sono viste dall'alto):

ora dobbiamo posizionare la telecamera (in inglese camera):

Riguardo alla telecamera bisogna indicare oltra alla posizione dove guarda, la cosiddetta Direzione della visuale (in inglese DOF o DOP):

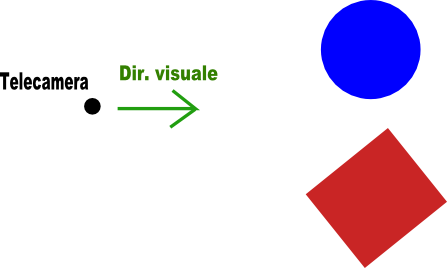
e bisogna dire qual e' l'alto per la telecamera. Se l'alto per esempio e' come vediamo le immagini, la sfera sara' a sinistra e il cubo a destra; se l'alto e' in basso avremo la sfera a destra e il cubo a sinistra. Se l'alto fosse a sinistra, avremmo la sfera sopra il cubo! Se ora non vi e' chiaro questo concetto, piu' avanti lo diventera'. Ora la telecamera e' correttamente definita:

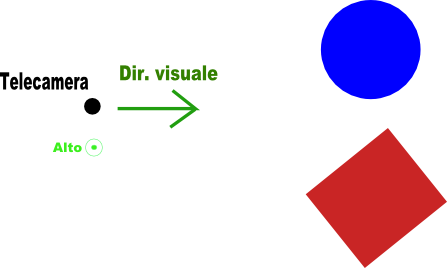
Ora dobbiamo pensare alla superficie bidimensionale che intercetta la proiezione della scena verso la telecamera, questa rappresenta lo schermo del PC. Questa superficie e' rettangolare, ha un'altezza, una larghezza e una distanza dalla telecamera, quest'ultima e' detta fuoco. La superficie bidimensionale e' sempre ortogonale al vettore della direzione della visuale e parallela al vettore che indica l'alto:

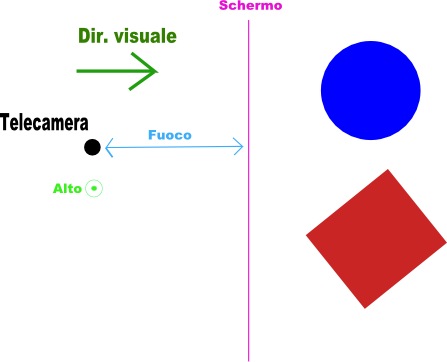
La preparazione per il passaggio in 2D è completa, ora basta tracciare le proiezioni degli oggetti verso la telecamera e avremo la nostra scena appiattita sullo schermo:

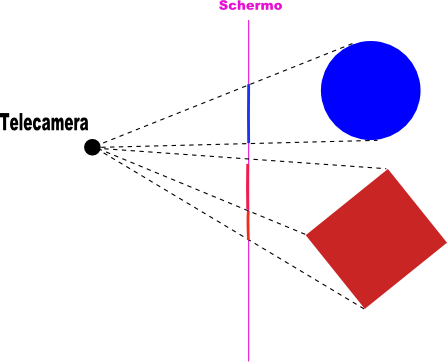
Se tutto è andato bene dovremmo ottenere il seguente risultato:

Che cosa e' il vettore V3? E' un vettore ortogonale al vettore Alto e al vettore Direzione visuale. Ci servira' piu' avanti.

Dal punto dei vista dei numeri abbiamo che quando posizioniamo gli oggetti e la telecamera siamo in un sistema di riferimento arbitrario che possiamo chiamare di partenza o mondo reale (in inglese lo chiamano anche world). Immaginiamo di aver piazzato la nostra telecamera nel punto C di coordinate (C_x, C_y, C_z).

Se immaginiamo la superficie dello schermo del PC come un piano x,y parallelo al piano alto,v3 , ci basta passare dal sistema di riferimento di partenza a quello centrato nella telecamera formato da alto,direzione visuale,v3 per avere le coordinate x,y dello schermo sul piano giusto. Per fare cio' basta creare la matrice di cambio di sistema di riferimento M cosi' fatta:

` [(v3_x,a l t o_x,DOF_x,C_x),(v3_y,a l t o_y,DOF_y,C_y),(v3_z,a l t o_z,DOF_z,C_z),(0,0,0,1)] `

quindi per avere le coordinate dei punti nel nuovo sistema di riferimento bisogna fare la seguente operazione:

` [(v3_x,a l t o_x,DOF_x,C_x),(v3_y,a l t o_y,DOF_y,C_y),(v3_z,a l t o_z,DOF_z,C_z),(0,0,0,1)]^-1 * [(X),(Y),(Z),(1)] = [(X_2),(Y_2),(Z_2),(1)] `

L'esponente -1 della matrice significa che bisogna farne l'inversione, un'operazione matriciale alquanto complessa. Graficamente il disegno sottostante spiega quello che si fa:

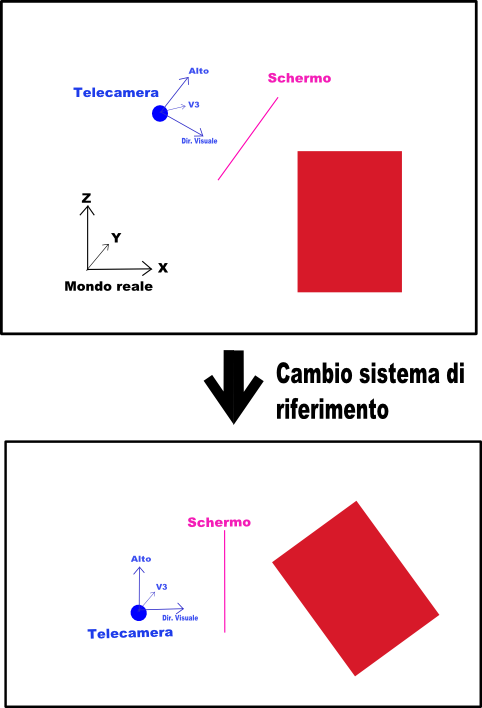
Ora le nuove coordinate x,y sono quelle che potremmo mettere direttamente sullo schermo, solo che vanno scalate a seconda della distanza dalla telecamera per fare una corretta rappresentazione. Qui ci sono due vie per trovare il coefficiente per scalare le coordinate.

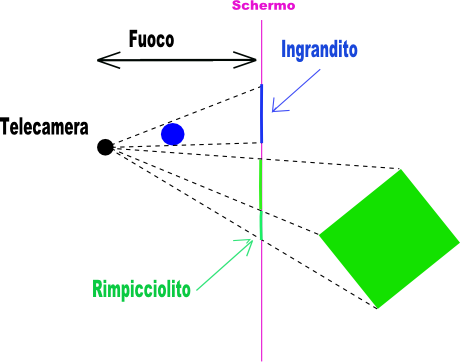
La prima, piu' rigorosa e corretta matematicamente, consiste nel dividere le coordinate dei punti per il rapporto ` z/f ` dove Z è la coordinata che rappresenta la distanza del punto dalla telecamera lungo l'asse della direzione di vista e f e' la distanza focale. C'e' un effetto curioso facendo cosi', gli oggetti che vogliamo rappresentare ma che si trovano tra la telecamera e lo schermo (dentro la lunghezza f fuoco) vengono ingranditi invece di essere rimpiccioliti. Ecco la spiegazioni grafica:

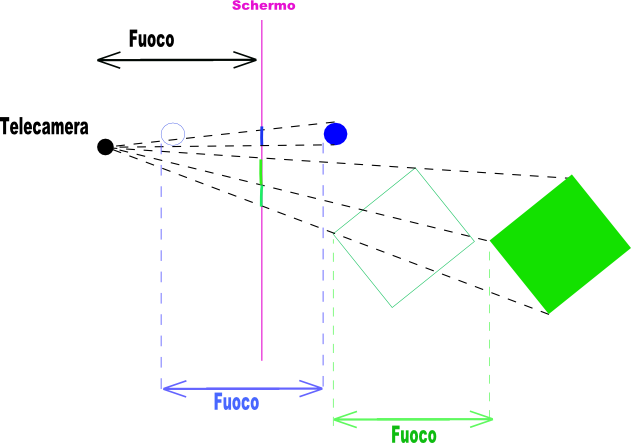
E' chiaro che la formula nasce solo per mostrare quello che e' dietro lo schermo, ma cosi' dovremmo calcolare cio' che e' dietro lo schermo e cio' che e' tra lo schermo e la telecamera. Per evitare di fare troppi conti si preferisce usare un trucco, cioe' utilizzare come coefficiente per scalare le coordinate il rapporto ` (z+f)/f `, che e' come traslare tutto lungo la direzione di vista di una lunghezza f (fuoco) in modo che non ci sia nulla tra la telecamera e lo schermo. Ecco il risultato:

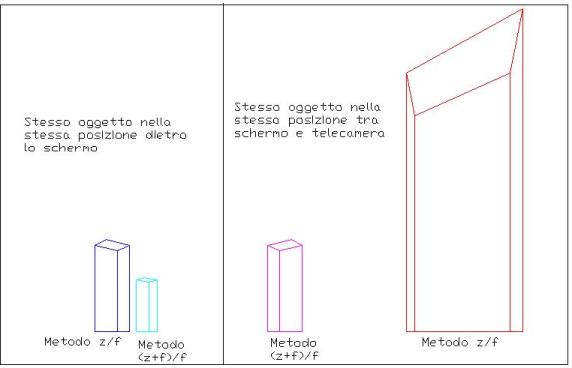
Usare il trucco e' lo stesso che usare la formula corretta? No. La vista cambia sensibilmente, ma per tutti gli oggetti che gia' si trovavano dietro lo schermo la differenza e' minima. Al contrario per gli oggetti tra lo schermo e la telecamere la prospettiva e' molto diversa. Comunque quasi tutti i programmi di 3D usano questo trucco. Ecco un esempio di come cambia la prospettiva dello stesso oggetto, notate come e' forte il cambiamento del parallelepipedo vicino alla telecamera: con il coefficiente ` z/f ` mostra quattro lati (deformazione prospettica), mentre con ` (z+f)/f ` ne mostra solo tre.

quindi potremmo scrivere:

` [(v3_x,a l t o_x,DOF_x,C_x),(v3_y,a l t o_y,DOF_y,C_y),(v3_z,a l t o_z,DOF_z,C_z),(0,0,0,1)]^-1 * [(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,1/f,1)] * [(X),(Y),(Z),(1)] = [(X_2),(Y_2),((Z + f)/f),(1)] `

In questo modo ilvettore ha gia' tutte le informazioni che ci servono per ogni punto: X,Y, fattore di scala.