Velocità E Accelerazione In Coordinate Polari
In coordinate polari un punto sul piano è individuato dalla distanza dall'origine e dall'angolo: ` P(r,theta) `
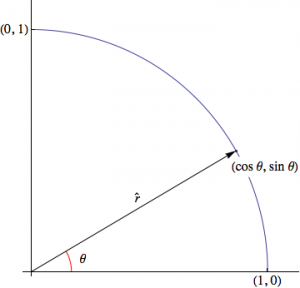
La velocità è la derivata della variazione di posizione rispetto al tempo:
` vec v= {d Delta vec s} / (d t) `
` { [v_r = {d r} / {d t }] , [ v_theta = r * {d theta} / {d t }] :} `
L'accelerazione e' la derivata della velocita':
` vec a = {d vec v} / {d t} `
` { [a_r = (d^2 r) / (d t^2) - r * ( (d theta) / (d t))^2 ] , [a_theta = 1/r * d / (d t) (r^2 * (d theta) / (d t))] :} `
Facciamo degli esempi pratici. Per calcolare la legge del moto nel tempo di un corpo sottoposto a delle forze, bisogna uguaglie m*a a tutte le forze agenti sul corpo.
Corpo sottoposto alla gravita' in scala umana
Se siamo sulla Terra e lavoriamo in una scala umana, la forza di gravita' si puo' approssimare con la seguente formula: ` F=m*g `; percio' per calcolare il moto lo sviluppo e' il seguente:
` m * a = m * g `
`a = g`
in coordinate cartesiane e':
` ddot y = g ` semplice equazione differenziale che si risolve integrando due volte
` y(t)= y_0 + v_y t + 1/2 g t^2 `
in coordinate polari e' identica:
` { [g = (d^2 r) / (d t^2) - r * ( (d theta) / (d t))^2 ] , [0 = 1/r * d / (d t) (r^2 * (d theta) / (d t))] :} `
poichè non varia su ` theta `:
` r(t) = r_0 + v_r * t + 1/2 g t^2 `
Legge di Hooke
Anche qui la legge della molla in verticale e' identica in entrambi i casi:
` m* ddot y = - k * y `
` ddot y = - k /m y ` oppure ` ddot r = - k /m r `
y e r sono identiche in questo caso. La soluzione generica sarebbe:
` y(t) = c_1 * sin (sqrt(k/m) * t) + c_2 * cos(sqrt(k/m) * t) `
Tensione di una corda che fa ruotare un sasso
Esaminiamo un altro caso semplice: un sasso allacciato ad una corda che lo fa girare. L'origine delle coordinate polari sara' la mano che tiene la corda e fa girare il sasso.
Vogliamo determinare la forza che agisce sulla corda sapendo il movimento che fà. Le equazioni del moto circolare uniforme polari sono (L e' la lunghezza della corda):
` { [r(t) = L], [theta(t)= omega * t] :} `
applicando le formule dell'accelerazione:
` a_r = (d^2 r) / (d t^2) - r * ( (d theta) / (d t))^2 = 0 - L * omega^2 = - L * omega^2`
` a_theta = 1/r * d / (d t) (r^2 * (d theta) / (d t)) = 1/L * d /(d t)(L^2 * omega) = 1/L * 0 = 0 `
la forza è solo radiale ed è uguale a ` F= - m_(s a s s o) * L * omega ^2 ` , piu' la velocita' di rotazione e' alta, piu' la massa del sasso e' grande o il cavo e' lungo, piu' la corda sara' sottoposta ad uno sforzo maggiore.
